Math “Coincidences”

Patterns often appear in math. Is it just a coincidence?

Impressively, many geometric functions can be drawn with just a straightedge and a compass.

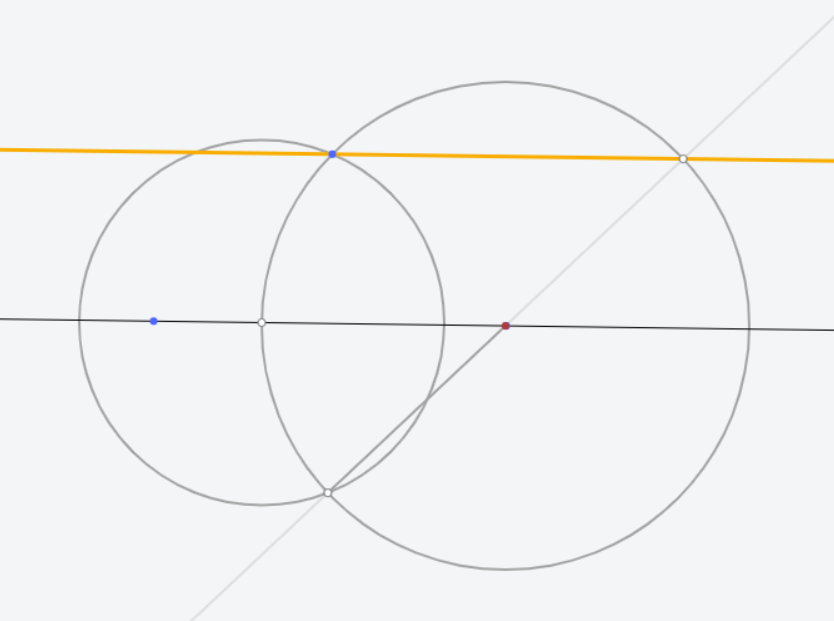
One such example would be constructing parallel lines. A parallel line can be constructed as follows: first, draw two circles centered on a line that intersect at two points. Use an intersection point and draw a line through one of the circle centers. When it intersects that circle again, use that point and the unused point to construct a new, parallel line (See Figure 1). Many more constructions are possible. In fact, there is a video game dedicated to it, Euclidea. However, while interesting, these don’t coincide with anything else. 

Instead, let’s look at a common function, combination. If we want to find the number of permutations using only two distinct characters, such as counting how many ways the four letters aabb can be ordered, out of four letters, two need to be picked as a or b. The number of ways to choose two out of the four is abbreviated as (4 nCr 2). The general formula for finding the value of (n nCr k) is n!/k!(n-k)! (the ! notation means factorial, so m! would equal m*(m-1)*(m-2) … *1).

Combinations appear in unexpected places. One such example is Pascal’s Triangle (See Figure 2), which is created by starting in row zero with just one and creating a new row by summing the two numbers that are above it. These numbers can be rewritten as a bunch of combinations, a seemingly unexpected coincidence (2)! Each term happens to match with a combination (row number nCr number in row). 

Combinations can also be applied to distributing items to people. A method called balls and urns (also known as stars and bars, sticks and stones, etc.) deals with distributing objects to different people or places. So given n people and k objects to distribute, the number of ways to distribute the objects is (n+k-1 nCr k). However, this does include giving unfortunate people no items at all. If everyone wants to be a winner, such that everyone gets at least one object, then the same method can be applied, just after everyone has been given 1 object.

While this may seem coincidental, the reason that combinations appear over a where combinations appear over and over again is molded into the same problem using clever methods. For Pascal’s triangle, the numbers can be thought of as coefficients of a binomial, (a+b)ⁿ, where a and b are variable and n is an integer. For example, the second row of Pascal’s triangle, 1 2 1, matches with (a+b)², which expands to 1a² + 2ab + 1b². If (a+b)² was multiplied out, instead (a+b)ⁿ⁻¹*(a+b) could be used, allowing the use of the previous expansion. If a previous expansion is used, each term can be multiplied by a and then added to those terms multiplied by b (See Figure 3). To expand (a+b)ⁿ in a different way, we can think of it as picking a or b for each term in (a+b)(a+b)…, since when multiplying this out, each (a+b) will provide either an a or b. 

Then, if each possibility of a or b per (a+b) is considered, the problem can be rewritten into a combination problem to find the coefficient of each term. For balls and urns, it is not as complicated. Simply say there are n people and k objects. To sort the objects, we can make dividers, specifically n-1 dividers to split the objects into n groups. Now, out of a total of k+n-1 things to sort, k must be chosen as the objects such that the rest are dividers (See Figure 4). Luckily, recurring uses of mathematical tools as combinations mean that the same notation can be used in a variety of different problems.

Appreciating math can be hard at first, but when math connections are made, it’s something to marvel at.

– Charlie Chen

References

1. “Combination.” Art of Problem Solving, artofproblemsolving.com/wiki/index.php/Combination.
2. “Combinations and Permutations.” Math Is Fun, www.mathsisfun.com/combinatorics/combinations-permutations.html.
3. “Euclidea.” Euclidea, www.euclidea.xyz/.
4. Benjamin, Arthur, and Natalya St. Clair. The Magic of Math: Solving for x and Figuring out Why. Basic Books, 2016.
5. Limited, Horis International. “Euclidea: Geometric Construction Puzzles v4.0 for IOS Devices Just Released.” PR Newswire: Press Release Distribution, Targeting, Monitoring and Marketing, 27 June 2018, www.prnewswire.com/news-releases/euclidea-geometric-construction-puzzles-v40-for-ios-devices-just-released-300577483.html.
6. Benjamin, Arthur, and Natalya St. Clair. The Magic of Math: Solving for x and Figuring out Why. Basic Books, 2016.

Images

1. https://www.euclidea.xyz/en/game/packs/Epsilon/level/Parallel
2. https://www.advancedhighermaths.co.uk/wp-content/uploads/2017/10/image/png/png/Binomial-Combination-2.png
3. https://docs.google.com/drawings/d/1367fNeffkanbYbC77UL5c4aM4aFHFsbl206AL3sCdEY/edit?usp=sharing
4. https://docs.google.com/drawings/d/120fF08xxt2nK5XDGUwa6VEiSCn2A6f12t0H9WdWKef8/edit