A mathematical model of a computer
In 1936, Alan Turing was a mathematics student researching probability theory at the University of Cambridge when he came across the Entscheidungsproblem (or “Decision Problem”). The Decision Problem asks the question of whether or not every mathematical problem can be solved with an algorithm (1, 2). This problem piqued his interest, and he resolved to solve it. Eventually, he was able to prove that it’s impossible to solve every mathematical problem with an algorithm. But more importantly, while solving this, he created a generalizable model of a computer – a model that is still used today in mathematical research. Modern computers are Turing machines, so all the math that applies to a Turing machine applies to the computers we use today as well (3).
At the time, the idea of computing was vastly different than how we think of it today. Digital computers didn’t exist, only mechanical ones, and they were far less powerful than the devices we use today (4). When Alan Turing created his model of a computer, he wasn’t thinking about today’s digital computers with transistors – rather, the bare bones of what computing is. A Turing machine has three parts: an infinite tape, the “head,” and a finite set of instructions for the head to execute (5). To apply these to a modern computer, you can imagine these as the memory, CPU (Central Processing Unit), and the program the CPU is running (6). A Turing machine works by having the head work through the program, reading and modifying the tape, until it reaches a halting state (5).
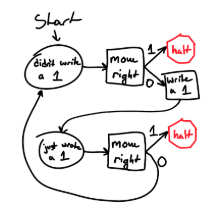
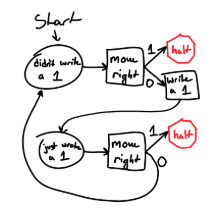
Imagine a Turing machine with the goal of turning the tape into a pattern of alternating 1s and 0s (i.e. “010101…”). In general, the tape of a Turing machine can contain anything, but it must have a defined set of allowed states for each cell (in this case, just 1 or 0). The head of this Turing machine has a finite number of possible states and a set of instructions on how to proceed through them in order to achieve our goal, illustrated in Figure 1. Then, the Turing machine executes the instructions with the given tape. For this program, you can see how the Turing machine would work on a short tape of “0001” in the Figure 2. It starts off by moving right, reading a 0 (which means that it should continue), and writing a 1 because the previous square was a 0. Then it moves right again, reads a 0 (so it knows to continue), and then moves right again since it knows it just wrote a 1 and shouldn’t in this square. Finally, it moves right again and reads a 0, so it stops there.
Understanding the mechanics of a Turing machine is a core piece of how mathematicians figure out what we can program our modern computers to do. Evaluating the limits of computers is key to many fields in computation. This is especially true in fields such as cryptography, where the strength of our encryption relies on the assumption that certain problems are too complex for our current computers to solve efficiently (7). Going forward, research using Turing machines will continue to be extremely useful as computers become more and more prominent in our lives. We will continue to need to know the limits of what our computers can do, and Turing machines offer an ability to figure this out, even as our computers become more and more advanced.
Bibliography:
- Copeland, B. (2024, August 25). Alan Turing. Encyclopedia Britannica. https://www.britannica.com/biography/Alan-Turing
- Pottenger, W. Morton , Swaine, . Michael R. , Hemmendinger, . David and Freiberger, . Paul A. (2024, August 31). computer. Encyclopedia Britannica. https://www.britannica.com/technology/computer
- Wolfram Science. (n.d.). What is a Turing Machine? Wolfram Science. Retrieved October 4, 2024, from https://www.wolframscience.com/prizes/tm23/turingmachine.html
- History of Computers. (n.d.). History of Computers: A Brief Timeline. History of Computers. Retrieved October 4, 2024, from https://historyofcomputers.eu/timelines/history-of-computers-a-brief-timeline/zz
- De Mol, L. (2018, September 24). Turing Machines. Stanford Encyclopedia of Philosophy. Retrieved October 4, 2024, from https://plato.stanford.edu/entries/turing-machine/
- Boyd, A. (n.d.). Inside the Machine. The Engines of Our Ingenuity. Retrieved October 4, 2024, from https://engines.egr.uh.edu/episode/2660`
- Henderson, T. (2013, November 11). Cryptography and Complexity. Hackthology. Retrieved October 4, 2024, from https://hackthology.com/cryptography-and-complexity.html




Comments are closed.